2025 大湾区拓扑会议

11月7–10日, 2025 | 华南师范大学（石牌校区） | 广州

Greater Bay Area Topology Conference 2025

The theme of GBATC2025 is algebraic topology and geometric topology, aiming to promote exchanges and collaborations among people in these two fields.

The organizers gratefully acknowledge the support by South China Normal University, and National Natural Science Foundation of China.

• 会议手册 • 会议海报 • 会议合影

Invited Speakers

(hint: click bolded talk titles to show abstracts)

苏阳, 中科院数学所

自复叠流形在环面上的纤维化 (Self-covering, finiteness, and fibering over a circle) 一个流形称为是自复叠的，如果它与自身的一个非平凡复叠同胚或同伦等价。环面是最简单的例子。对于具有交换基本群的自复叠闭流形，我们研究了它是否可以作为环面上的纤维丛的问题。在不同条件下，既得到了正面的结果，也发现了反例。这是和秦理真，王博潼合作的工作。

slides

于立, 南京大学

On simplicial complexes with maximal total Betti number and total bigraded Betti number The total Betti number (i.e. the sum of all the Betti numbers) of a space measures the topological complexity of the space and plays important roles in many theories in mathematics. In this talk, we first classify those simplicial complexes with a given number of vertices that have the maximal total Betti number. Then we study similar problems for the sum of bigraded Betti numbers. It is known that the sum of bigraded Betti numbers of a simplicial complex K with m vertices is bounded from below by $2^{m-dim(K)-1}$. We discuss the classification of all the simplicial complexes with m vertices that have the maximal or the minimal sum of bigraded Betti numbers, respectively.

slides

陈波, 华中科技大学

On the homology description of equivariant bordism groups of n+1 dimensional $\mathbb{Z}_2^n$-manifolds with isolated fixed points set We construct a chain complex $\mathfrak{B}$ based on a double complex derived from the universal complex $X(\mathbb{Z}_2^n)$. It is shown that $\mathfrak{B}$ has a nontrivial homology only in degree $n-2$, which is isomorphic to the equivariant unoriented bordism group $\mathcal{Z}_{n+1}(\mathbb{Z}_2^n)$ of all $(n+1)$-dimensional smooth closed $\mathbb{Z}_2^n$-manifolds with isolated fixed points. By analyzing the spectral sequence of $\mathfrak{B}$, we derive a dimension formula for $\mathcal{Z}_{n+1}(\mathbb{Z}_2^n)$ as a $\mathbb{Z}_2$-vector space, which agrees with a recent result for $n=3$.

slides

陈亮, 东北师范大学

On curvatures of singular mixed-type surfaces in Lorentz-Minkowski 3-space We embark on an exploration of the differential geometric properties of singular mixed-type surfaces in Lorentz-Minkowski 3-space. Generally speaking, a mixed-type surface is defined as a connected regular surface that features non-empty sets of spacelike and timelike points. To facilitate our study, we introduce a valuable tool known as the modified frame on the surface. As a result, we reveal the behavior of the Gaussian curvature and the mean curvature of the singular mixed-type surface at not only lightlike points but also singular points.

朱中坚, 温州大学

Homotopy types of $(2k-1)$-sphere bundles over $2k$-sphere The classification problem of sphere bundles over spherical spaces, in terms of homotopy and homeomorphism, is a classical topic in the classification of manifolds. It plays an important role in topology and geometry. For example, Milnor showed that the total spaces of $S^3$-bundles over $S^4$ with Euler class ±1 are manifolds homeomorphic to $S^7$ but not always diffeomorphic to it. In this talk I will introduce our recent work on classifying the homotopy types of the total space of $(2k-1)$-sphere bundles (fibrations) over $2k$-sphere. These are joint works with Professor Jianzhong Pan.

slides

郑芳婷, 西交利物浦大学

Discrete embeddings of hyperbolic groups with Pontryagin surfaces as boundaries In this talk, I will exhibit some convex cocompact, discrete subgroups $\Gamma_2$ and $\Gamma_3$ in the isometry group of 5-dimensional hyperbolic space H^5, whose limit sets are the index-2 and index-3 Pontryagin surfaces $\Pi_2$ and $\Pi_3$, respectively. This result yields new, distinct topological types of limit sets for higher-dimensional Kleinian groups. This is joint work with Jiming Ma.

李平, 复旦大学

The compactification of homology cells, Fujita's conjectures and the complex projective spaces Hirzebruch在1954年的问题集中有两个问题关心复欧式空间的紧化和复射影空间的唯一性。Takao Fujita在1980年这两个问题加强成三个密切相关的猜想。在此报告中，我们将回顾这些历史并讲述近期的一些进展。此报告中的部分工作是与Thomas Peternell合作的。

slides

古星, 西湖大学

Topological complexity of enumerative problems in algebraic geometry Typical enumerative problems in algebraic geometry includes finding the d roots of a generic polynomial in one variable of degree $d$, and finding the $27$ lines on a smooth cubic surface. We introduce the concept of topological complexity of enumerative problems, which is a positive integer that measures the least possible number of “branches” in the algorithms that solves an enumerative problem up to an $\varepsilon$ error. We are interested in the lower bounds of the topological complexity of enumerative problems. We introduce finite covering spaces associated to the enumerative problems and the concept of Schwarz genus of a covering space, which produces lower bounds of the topological complexity, and can be detected by cohomology. Finally, we present lower bounds of three enumerative problems. This is a joint work with Weiyan Chen.

slides

Schedule

周六，11月8日, 数学西楼111报告厅

8:40~9：30 | 苏阳（中国科学院） 自复叠流形在环面上的纤维化
9:30 茶歇与会议合影
10:00~10：50 | 于立（南京大学） On simplicial complexes with maximal total Betti number and total bigraded Betti number
10:00~10：50 | 陈波（华中科技大学） On the homology description of equivariant bordism groups of n+1 dimensional $\mathbb{Z}_2^n$-manifolds with isolated fixed points set ---
12:00~14：30 | 午餐、午休
14:30~15：20 | 陈亮（东北师范大学） On curvatures of singular mixed-type surfaces in Lorentz-Minkowski 3-space
15:20~15:40 | 茶歇
15:40~16：30 | 朱中坚（温州大学） Homotopy types of $(2k-1)$-sphere bundles over $2k$-sphere
16:50~17：40 | 郑芳婷（西郊利物浦大学） Discrete embeddings of hyperbolic groups with Pontryagin surfaces as boundaries
18:00~ | 晚餐

周日，11月9日, 数学西楼111报告厅

9:30~10：20 | 李平（复旦大学） The compactification of homology cells, Fujita's conjectures and the complex projective space
10:50~11：40 | 古星（西湖大学） Topological complexity of enumerative problems in algebraic geometry
12:00~17：00 | 午餐、自由讨论

Local information

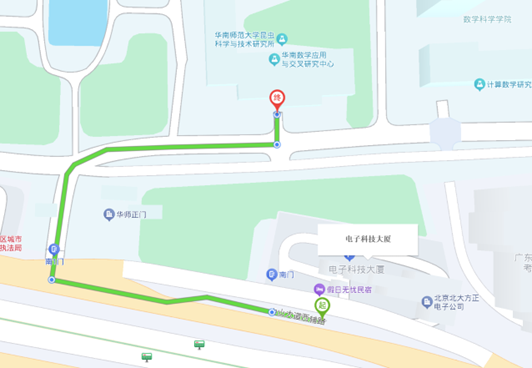
从酒店步行到华南师范大学数学学院西楼路线图， 全程200米，约3分钟：

Organizers

会议联系人:

If you have any questions, comments or suggestions, please contact us at gba.topology@outlook.com

Participants

Updated Nov. 3， 2025：